
反向传播的目的是计算成本函数C对网络中任意w或b的偏导数。一旦我们有了这些偏导数,我们将通过一些常数 α的乘积和该数量相对于成本函数的偏导数来更新网络中的权重和偏差。这是流行的梯度下降算法。而偏导数给出了上升的方向。因此,关于反向传播算法,我们继续查看下文。
我们向相反的方向迈出了一小步——下降的方向,也就是将我们带到成本函数的局部最小值的方向。
图示演示:
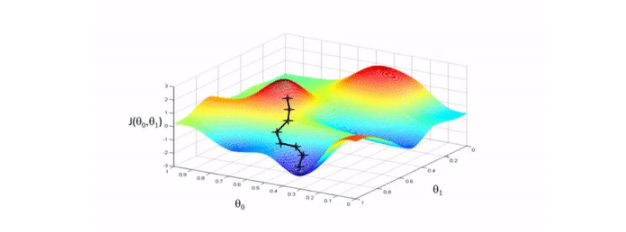
反向传播算法中Sigmoid函数代码演示:
# 实现 sigmoid 函数 return 1 / (1 + np.exp(-x)) def sigmoid_derivative(x): # sigmoid 导数的计算 return sigmoid(x)*(1-sigmoid(x))
反向传播算法中ReLU 函数导数函数代码演示:
def relu_derivative(x): # ReLU 函数的导数 d = np.array(x, copy=True) # 用于保存梯度的张量 d[x < 0] = 0 # 元素为负的导数为 0 d[x >= 0] = 1 # 元素为正的导数为 1 return d
以上内容,相信可以让我们更好地了解了反向传播的实际效果。既然现在我们已经了解了反向传播实际上在做什么,那就进行实际的应用吧~









